방정식이란 말은 다들 들어봤을 것임. 까먹었을 수야 있겠지만 확실히 들어는 봤을 거임.
반면, 미분방정식이라는 말은 못 들어봤을지도 모름. 이공계 대학생이었다면야 어지간해서는 들어봤을 거지만, 모두의 인생에 있어서 반드시 들어봤을 것이라는 보장이 있는 단어는 아님.
그런 의미에서 간단하게 의미를 설명하자면, 미분이 들어있는 방정식임. 미분은 수가 아니라 함수에 하는 것이기 때문에 자연스럽게 미분방정식은 "이를 만족하는 값"을 찾는 것이 목적이 아니라, "이를 만족하는 함수"를 찾는 것이 목적이 됨.
여기 미분 방정식이 하나 있음
상수를 굳이 c^2으로 쓴 것은 반드시 양수라는 것을 강조하는 의미도 있지만, 이 방정식의 의미와도 연관되어 있음. 자세한 내용은 후술
이 편미분 방정식은 양변을 보면 f를 x로도 두 번 편미분하고 t로도 두 번 편미분하고 있음. 따라서 이 방정식을 만족하는 f를 찾고자 한다면, 당연하지만 f는 t로도 x로도 두 번 편미분 가능해야함. 이는 당연한 소리임.
이런 것은 다른 방정식 문제를 풀 때에도 항상 조심해야 하는 것임. 방정식을 풀 때 식 조작은 대체로 해의 가능성을 좁히기 위한 수단이고, 최종적으로는 이를 원래 방정식에 대입해서 실제로 만족하는 지를 확인해야 하는 경우가 많음. 만약에 기하학적인 문제를 풀기 위해서 방정식을 설계했거나 한다면 당연히 해 중에서 실제 기하학적인 성질을 잘 만족하는 지 검토해야 할 것임. 길이가 음수가 나왔다거나 하다면 "길이가 음수"라는 답을 내는 것이 아닌 "그런 것이 존재하지 않는다"라는 결론을 내야 할 것임.
실제로 이것과 관련된 유명한 사건으로 수능 생명과학 II 출제 오류 사건을 들 수 있음. 방정식이 단순히 문제를 위해 만들어진 것이라면 모르겠지만, 현실의 문제를 모델링한다면, 얻은 답이 실제 문제를 잘 표현하는지 확실하게 확인할 필요가 있음.
그런 의미에서 위의 방정식의 해는 당연히 미분 가능해야함. 방정식에 미분을 하고 있으니까!
라고 끝낼 것이면 이 글을 쓰지 않았을 것임. 왜냐하면 이 방정식은 단순히 저것을 풀고 싶다! 하고 임의로 만든 방정식이 아니라 현실을 모델링하기 위해 구상된 방정식이기 때문임.
위 방정식은 1차원 파동 방정식이라고 불리는 방정식으로, 말 그대로 1차원 파형이 시간에 따라 어떻게 움직이는지 해석하기 위한 방정식이며, 상수 c는 매질의 속도에 해당하는 상수임. 이 방정식은 경계 조건, 초기 조건에 따라 이런저런 풀이법과 해를 가지는데, 여기서는 달랑베르 해를 소개할 것임. 이는 초기 상태, 즉 시간 t=0인 경우 파동의 모양 g(x)와 외부 움직임 h(x)가 주어졌을 때 해에 해당함. 현실적인 상황에 있어서도 지극히 자연스러운 상황이라고 할 수 있음.
풀이법은 생략하고 해만 소개하자면,
이렇게 생긴 해를 가진다는 것이 알려져 있음. 앞부분을 보면 x-ct, x+ct는 다른 게 아니라 시간이 흐름에 따라서 속도 c로 움직이는 것을 표현하고 있음. 처음 파동이 +방향과 -방향 양쪽으로 동시에 움직이기 때문에 반으로 나눠져서 절반은 +방향, 나머지 절반은 -방향으로 움직이는 것이 잘 표현되어 있음
뒤의 적분 항은 초기에 주어진 외부 움직임이 영향을 주는 것이 속도 c로 제한된다는 것을 표현하는 요소이기도 함. 즉 이 방정식은 실제로 파동의 물리적인 성질을 어느 정도 잘 표현하고 있음.
위의 식을 잘 보면, 딱히 여기서 g와 h에 대해서는 미분 가능성을 요구하고 있지 않음. 애초에 미분하지 않기 때문. 따라서, 수학적으로는 이상한 소리가 될 것처럼 보이지만, 만약 g와 h가 미분 불가능한 함수로 주어진다고 해도, f 자체는 잘 정의됨. 단지 미분 불가능하다는 사소한(?) 찐빠가 있을 뿐. 따라서 g, h가 미분 불가능하면 해는 없다! 라고 하기에는 위 식은 너무 파동의 움직임을 잘 설명하고 있음.
위에서 말했듯, 미분방정식은 단순하게 해를 구하는 것을 넘어서, 현실 문제를 잘 표현하는지를 검토할 필요가 있음. 이 사실이, 이번에는 반대로, 이 방정식은 해가 없다! 하고 그냥 넘기지 못하게 만드는 것. 만약 현실 파동의 움직임이 실제로 미분 불가능한 모양이라면? 그러한 경우에 미래를 예측하고자 한다면, 위의 해가 설령 미분 불가능하다고 하더라도 해로 인정하고 분석하는 것이 의미가 있지 않을까?
따라서, 수학적으로 미분 불가능하다고 하더라도 단순히 해가 없음이라 넘기지 않고 저런 것을 일종의 "해"로 다루기 위한 설명을 붙이고자 하는 시도도 당연히 존재하게 되었음. 그에 대한 답 중 하나로, "약한 해"를 들 수 있음. 엄밀하게 설명하자면 분포부터 시작해서 자세하게 설명해야 하지만, 간단하게 설명하자면, 위 방정식을 일종의 적분 형태로 변형하는 것임. 위의 파동 방정식을 예시로 들자면, 위 방정식 대신에
이렇게 생긴 적분방정식을 풀게 됨. 이 방정식은 단순히 한 Φ에 대해 푸는 것이 아니라, 모든 유한 영역에서만 값을 가지고 무한번 미분 가능한 함수에 대해서 만족하게 풀어야 함. 이 방정식은 애초에 f를 전혀 미분하고 있지 않기 때문에 이 방정식의 해는 미분 가능한 함수일 필요가 없음. 그리고 위에서 구한 해는 실제로 위 방정식을 만족하는 것을 알 수 있음. 따라서 초기 조건이 미분 불가능하다고 하더라도, 미분 불가능한 약한 해가 현실을 잘 모델링한다고 할 수 있음.
이렇듯, 미분 불가능하다면 그것으로 끝이 아니라, 이것이 가지는 의미를 분석하고자 하는 것 또한 중요한 연구과제가 될 수 있음. 실제로 교통 체증 분석도 이런 미분 불가능성과 조금 연관이 있음.
구체적으로 방정식을 제시하는 것은 기회가 된다면 나중에 해보고 간단하게 얘기하자면, 교통량을 미분방정식으로 모델링을 해 보면, 초기 조건에 따라 해당 방정식의 해는 미분 불가능해지는 특이점을 가지게 됨.
이에 대해서 수학적으로 간단하게 때운다면야 특정 영역 내에서만 해를 가지게 된다로 끝낼 수도 있지만, 미분 불가능하다는 것이 일종의 불연속성을 가리키게 된다는 것을 인식하게 된다면 얘기는 더 확장됨.
이 미분 불가능해지는 점, 즉 속도가 급하게 변하는 상황이 도로 교통량에 있어서 무슨 의미를 가질 지 생각해보면 의외로 답은 꽤 명확한데, 이 미분 불가능해지는 점이 바로 "교통 체증이 시작되는 점"이 됨. 길이 막히는 상황을 상상해보면, 여태까지는 잘 달리고 있다가 갑자기 앞차들이 서 있는 지점을 마주하게 되고, 그 뒤로는 뭔가 상황이 해소될 때까지 느릿느릿 나아가게 됨. 여기서 앞차들이 서 있다는 것이 무슨 의미인가 하면, 차들의 밀도가 갑자기 변하는 지점이고, 이 같은 상황이 바로 미분 불가능성으로 나타나게 된다고 해석할 수 있다는 것.
1. 미분 불가능성 조차도 수학적으로는 연구 대상이 될 수 있음
2. 물리적으로 실재하는 것을 설명하기 위해서 반대로 수학을 설계하는 경우도 있음
3. 즉, 수학도 때로는 약팔이에 뒤치다꺼리 재능이 필요함
4. 원래 지난주에 올리려고 했는데 게시판이 화끈한 떡밥으로 불타고 있길래 그만......

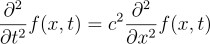
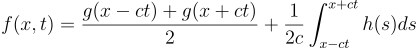
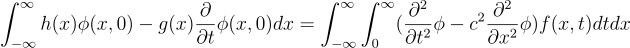
(IP보기클릭)121.130.***.***